- Welcome to the Kancolle Wiki!
- If you have any questions regarding site content, account registration, etc., please visit the KanColle Wiki Discord
Difference between revisions of "Air Reconnaissance"
Jump to navigation
Jump to search
Jigaraphale (talk | contribs) m |
m (Map filename) |
||
| Line 1: | Line 1: | ||
<noinclude>Air Reconnaissance is a mechanic seen on [[6-3]] that enables a chance at increased resources from specific nodes with the use of Seaplanes. | <noinclude>Air Reconnaissance is a mechanic seen on [[6-3]] that enables a chance at increased resources from specific nodes with the use of Seaplanes. | ||
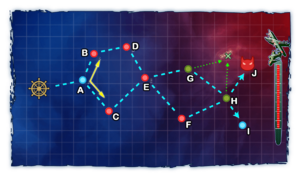
| − | [[file:6- | + | [[file:World 6 6-3 Map.png|right|thumb|300px|An example of recon nodes on map 6-3]] |
[[file:AirReconGet.png|right|thumb|250px|Air recon success shown after boss node win]] | [[file:AirReconGet.png|right|thumb|250px|Air recon success shown after boss node win]] | ||
Revision as of 07:57, 10 November 2022
Air Reconnaissance is a mechanic seen on 6-3 that enables a chance at increased resources from specific nodes with the use of Seaplanes.
Details
On Nodes G and H, Seaplanes will be flown towards the "green X" (the recon route is shown on the map as green arrows).
- Successful reconnaissance will reward additional resources upon getting a B+ rank on the boss.
- Neither G or H have combat.
- Animation will be shown for the Air Reconnaissance; if both
 Large Flying Boats
Large Flying Boats
 and other
and other  Seaplanes (SPR and SPB) are brought, Flying Boat animation takes priority.
Seaplanes (SPR and SPB) are brought, Flying Boat animation takes priority. - Success rate of the air reconnaissance depends on the LoS and Seaplanes count.
- All reconnaissance rewards are forfeit if the boss node is not reached or losed.
The formula for Air Reconnaissance is [math]\displaystyle{ R = \sum_{\text{SPR ; SPB}} \text{LoS} \times \sqrt{\sqrt{\text{Plane}_\text{Count}}} + \sum_{\text{Flying Boats}} \text{LoS} \times \sqrt{\text{Plane}_\text{Count}} }[/math]
To sum up, the more LoS and Seaplanes used, the better, with Flying Boats counting for more than other seaplanes.
- The minimum "[math]\displaystyle{ R }[/math]" to achieve success is 12 for G and 16 for H.
- For Great Success, the requirement is [math]\displaystyle{ R_\text{GS} = R \times (1.6 + rand(0 ; 0.6)) }[/math].
- This means that the minimum and maximum requirement for Great Success for H is 25.6 and 35.2.
See Also
| |||||||||||||||||||||||||||||||||||||||||||||